Find out how you can use technology to engage students in rich learning experiences.
Editor's Note: Dr. Puentedura developed the SAMR model in 2010, and wrote this article in 2014. The SAMR model is still referenced and recommended today.
For teachers just starting out with educational technology, the task can sometimes seem daunting. Even though tools such as the SAMR model can help, the choices available can prove paralyzing, frequently resulting in uses of the technology that block, rather than enable, more ambitious transformative goals.
The approach below is designed to help overcome this barrier, and is inspired in its form by Alexander’s notion of Design Patterns—a clearly structured solution to a recurring design problem—which has been applied to education scenarios by Bergin et al. While it's not laid out exactly as a design pattern would be, it nonetheless provides a useful framework.
The goal for the teacher is to construct a simple SAMR ladder that is coupled to Bloom’s Revised Taxonomy: As the task moves from lower to upper levels of the taxonomy, it also moves from lower to upper levels of SAMR. The two Enhancement levels of SAMR (Substitution, Augmentation) are associated with the three lower levels of Bloom (Remember, Understand, Apply), while the two Transformation levels of SAMR (Modification, Redefinition) are associated with the upper levels of Bloom (Analyze, Evaluate, Create). Within each grouping a similar ordering occurs: Remember-type tasks are primarily associated with S-level uses of the technology, Understand-type tasks are associated with either S- or A-level uses of the technology, and so on. The following diagram illustrates this association.
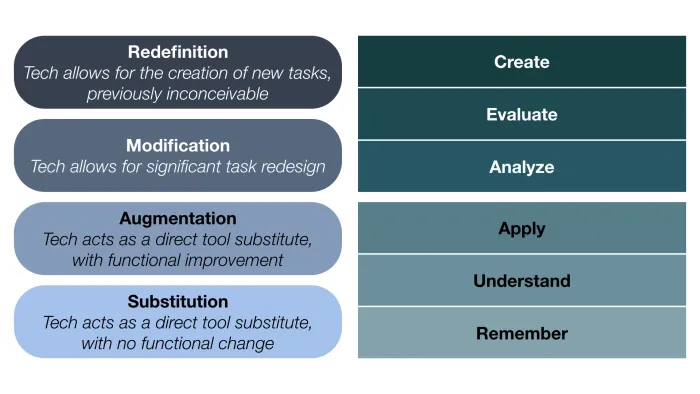
This coupling of the SAMR model and Bloom’s Taxonomy has several desirable outcomes:
- The already-familiar drive to reach the upper levels of Bloom’s Taxonomy now also acts as a drive to reach the upper levels of SAMR.
- It outlines a clear set of steps that help guide the introduction of technology in the classroom.
- It helps avoid pitfalls of self deception, like assuming that a particular task is at a higher level in either the Bloom or SAMR sense than it actually is.
It's important to realize that this association between SAMR and Bloom’s Taxonomy isn't necessary all the time. For example, it's possible to use extremely powerful redefinition-level approaches to make certain types of memorization tasks possible. And it's also possible to undertake novel create-type tasks that only make basic substitution/augmentation use of the technology. Additionally, far more complex couplings between SAMR and Bloom are possible, involving convergent/divergent branchings, oscillations between levels, skipping of some SAMR levels, etc. But the simple structure described above is a solid place to start.
In addition to the integration of SAMR and Bloom described above, two more ingredients are necessary for the best results:
- Have a clear motivation for the change: The best results happen when a teacher has a strong reason for changing existing practice that's independent of the introduction of technology.
- Have a clean app flow that's as simple as possible, avoiding needless complexity, as in transferring work products from one app to the next.
Finally, let’s look at an example of this approach in practice. In this example, we'll set up a general pattern for math activities, where the motivating factor is to take math instruction from a mode where—to use Richard Skemp’s words—instrumental understanding dominates ( just the "how") to a mode where relational understanding is primary (both "how" and "why"). This shift in math instruction can be seen in changes in curricula worldwide, and is crucial to students’ capacity to use—and enjoy—the math they've learned in the world outside the classroom. To make the example more tangible, imagine the course is introductory statistics (though the general pattern applies to other math courses).
1. Substitution/Remember: Students use ebooks and other Open Education Resources to acquire basic knowledge about statistical tools and procedures.
2. Substitution/Understand: At the same time, they begin a process of gathering information online describing applications of these statistical tools to an area of interest to them, using simple bookmark aggregation services (e.g., Diigo, Scrible) to collect and tag these resources, relating them to the knowledge gained in the first step.
3. Augmentation/Apply: Using a simple yet powerful tool for visualization like GeoGebra, students explore the concepts covered in the resources they collected in the previous steps, and solve related standard problems. The scope and number of the problems isn't about what's available in the “back of the book,” but rather driven by the evolution of student understanding, as measured by suitable formative assessment processes.
4. Modification/Analyze: The students also apply similar problem-solving approaches to questions raised in the materials they found in step two. In doing so, they'll reconstruct the reasoning of the original authors, and verify—or disprove—their conclusions.
5. Modification/Evaluate: Students now select a subset of the materials studied in step four for further critique and/or development, using GeoGebra as their primary analysis tool. Then, they explain this work to fellow students, and invite their feedback to refine both the clarity of their explanations and the focus of their work.
6. Redefinition/Create: Students refine their explanation into a short digital video project, with the goal that it will be used as part of instructional materials in subsequent years.